本人能力有限,翻译只是为了更好的理解,如有错误欢迎指正!
本文翻译自《Going Deeper into Regression Analysis with Assumptions, Plots & Solutions》
介绍
在预测模型中,回归分析经常是第一步骤。毋庸置疑,回归分析应用起来非常简单,语法和参数都不会引起任何混淆。 但是仅仅只是运行一行代码,并不能解决实际的目的。不要只是观测R^2或MSE值,回归分析能告诉我们更多的信息。
利用R中函数plot(model_name)返回回归分析的四张图。每张图都能提供关于数据的显著信息或展现一个非常有趣的故事。 悲哀的讲,很多初学者都不会解读这些信息或不关心这些信息。一旦你理解了这些图的含义,你的回归模型的预测能力 将有一个显著的提升。
为了改进模型,你也需要理解回归模型的假设和当违反假设时的解决方法。
在这篇文章中,作者会解释这些图和重要的假设来帮助你更详尽的理解回归的概念。就像上面所说的,理解了这些东西, 你能极大的提高模型的预测能力。
注意: 为了理解这些图信息,你必须具备回归分析的基础知识。如果你是初学者,你可以先阅读这篇文章。
回归假设
回归是一种参数方法。‘Parametric’意味着需要根据分析的目的对做出相应的假设。由于它参数化的一方面,因此回归模型在本质上是有限制。 如果数据集不满足回归模型的假设,回归模型将不能产生很好的预测结果。因此,对于一个成功的回归分析,去验证数据集是否满足回归分析的假设是十分有必要的。
下面是回归分析的重要假设。
- 自变量和因变量间应该存在一个线性加和的关系。一个线性关系意味着X每改变一个单元,响应变量的每次改变是固定值。一个加和关系意味着自变量对因变量的影响是相互独立。
- 残差项不相关。否则表示残差项存在自相关现象。
- 自变量不相关。否则表示自变量存在多重共线性。
- 残差项具有固定方差。否则表示回归模型具有异方差。
- 残差项必须符合正态分布。
如果违反了这些假设会怎么样?
让我们深入这些假设并了解违反这些假设产生的结果。
1.线性加和: 如果你用线性模型拟合非线性可加的数据,回归模型不能捕获数据的数学趋势,因此会产生一个低效的模型。同时,这个模型会在测试数据上产生错误的预测结果。
如何检测: 查看残差和拟合值的图(下面会解释)。同时,你可以尝试使用多项式模型拟合你的数据集。
2.自相关: 残差项具有相关性会极大的降低模型的准确度。这种情况经常发生在时间序列模型中(下一个时间段的变化依赖于上一个时间段的变化)。如果残差项具有相关性, 估计所得的标准误差会比实际标准误差小。
残差项自相关会使置信区间和预测区间变窄。窄的置信区间意思是一个95%的置信区间的实际概率会比真实的95%的置信区间的概率小(比95%小)。下面是窄区间的例子:
例如,自变量x1的最小二乘系数是15.02,标准误差是2.08(无自相关性)。但是由于自相关性的存在导致标准误差变为1.20。因此,预测区间由(12.94, 17.10)变为(13.82, 16.22),变窄了。
同时,较低的标准误差会使p值变小,这会使我们得到一个错误的显著参数。
如何检查: 查看DW统计值。它必须在0和4之间。如果DW=2,表示无自相关。如果0<dw<2,表示负相关;2<dw<=4,表示正相关。同时你也可以看残差和时间图来看残差值间的季节或相关的模式。
3.多重共线性: 表示自变量间存在中度或高度的相关性。模型中存在相关变量,会很难发现预测变量和响应变量间的关系。换句话说,多重共线性会导致我们很难发现哪个变量对预测更有价值。
另一点,多重共线性会使标准误差变大。同时,大的标准误差会使置信区间变大,导致斜率估计值的精确度变小。
同时,当自变量是相关的,模型中的一个相关变量的系数会依赖于其他变量。如果这种情况发生,你最终会得到一个错误的结论,一个变量会或强或弱的影响着目标变量。因此,即使4你删除一个相关变量, 估计的回归系数也会改变,这并不是一个好结果。
如何检测: 你能用三点图来可视化变量间的关系。同时你也可以使用VIF因子,如果VIF<=4,无多重共线性;如果VIF>=10,具有严重的多重共线性。总之,一个相关表可以解决问题。
4.异方差: 残差项无固定方差造成异方差。通常,异常值是异方差出现的原因。看起来像是这些值(异常值)具有很大的权重,因此对模型的表现造成不成比例的影响。如果存在异方差,会使置信区间变得非常大或非常小。
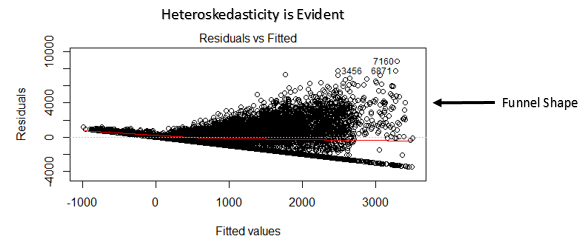
如何检测: 你可以看残差和拟合值的图。如果存在异方差,图会是一个漏斗的形状(下面会有解释)。同时,你可以用Breusch-Pagan / Cook – Weisberg test or White general test来检测异常差。
5.残差项无正态分布: 如果残差项不符合正态分布,置信区间会非常大或非常小。一旦置信区间不可靠,它会使最小二乘法估计系数变得困难。残差项不符合正态分布显示数据中存在一些不寻常的点,我们可以通过研究这些 不寻常的数据来使模型表现的更好。
如何检测: 你可以用QQ图(下面会有解释)或使用Kolmogorov-Smirnov test, Shapiro-Wilk test来检测。
回归图的解释
1. Residual vs Fitted Values(残差VS拟合值)
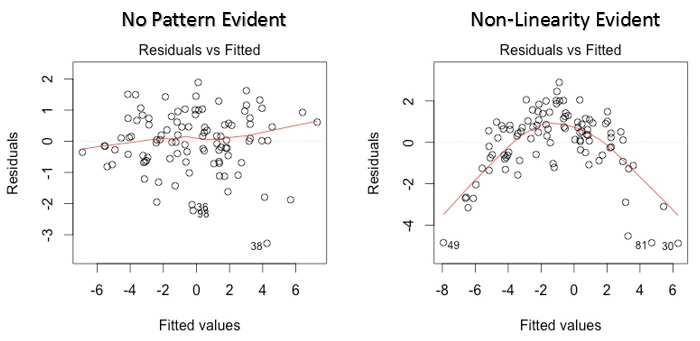
散点图展示了残差和拟合值的分布。它包含很多有用的东西,包括发现异常值。异常值在图中被标记了数据集中的位置。
这有两个主要的情况需要我们了解:
- 如果在图中存在任何的形状(可能是个抛物线),把它考虑作为数据是非线性的标志。这意味着模型不能捕获非线性效应。
- 如果图中是一个明显的漏斗形,把它考虑作为残差无固定方差的标志,例如异方差。
解决方法: 为了解决非线性问题,你可以对自变量进行非线性转换(log (X), √X or X²)。为了解决异常差问题,你可以尝试转换相应变量为log(Y) or √Y。同时你可以使用加权最小二乘法来处理异常差问题。
2.Normal Q-Q Plot(正态qq图)
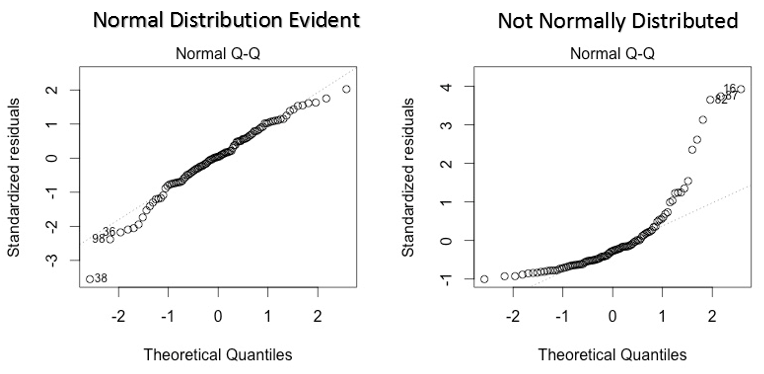
qq图是一个散点图来帮助我们检验数据是否来自正态分布。如果数据集来自正态分布,那么图是一条直线。偏离正态分布的误差可以在与直线的偏差中看到。
如果你好奇什么是分位数,这里有一个简单的解释:
解决方法: 如果残差项不符合正态分布,变量(自变量或因变量)的非线性转换能提高模型的表现。
3.Scale Location Plot

这个图可以用来检测异常差(假设方差想等)。它可以展现残差在预测范围中是如何分布的。它和residual vs fitted value plot相似,只不过这里使用的是标准化残差。 理想的话在图中没有任何明显的模式,这表示残差是正态分布的。如果在图中表示出任何形状,例如例子中的漏斗形,这表示残差不符合正态分布。
解决方法: 可以用图1中解决异常值的方法来解决。
4. Residuals vs Leverage Plot 分位数是按大小顺序表示一定比例的数据点。分位数通常被称为百分位数。例如:50百分位数是120,意思是一半的数据比120小。
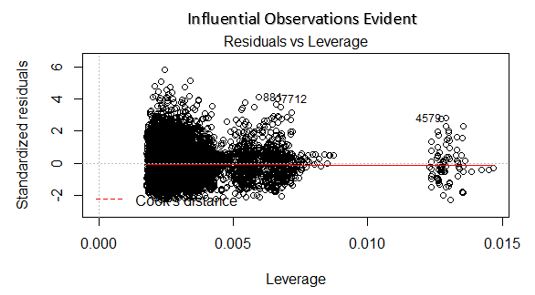
这个也被叫做Cook’s Distance plot。Cook’s distance尝试定义数据点的影响力。影响力大的点会对回归线有非常大的影响。换句话,添加或删除这样的数据会完全改变模型的统计意义。
这些影响力非常大的点可以当做异常值来处理吗?这个问题只能再进一步查看数据后回答。因此,在这个图中,影响力大的值需要进一步的分析。
解决方法: 如果这些值不多,可以删掉。作为选择,你可以根据数据中的最大值按比例缩小异常值或把这些值当做缺失值。