A/B Testing, from scratch——翻译

本人能力有限，翻译只是为了更好的理解，如有错误欢迎指正！

介绍

A/B测试是一项的随机对照实验，并在实验中比较两种产品变量的表现。这些变量通常用变量A和变量B来表示。从商业角度来看我们想知道某个变量的表现是否优于其他变量。

例如我们想评估在结账页面中绿色的结账按钮是否优于橙色结账按钮。

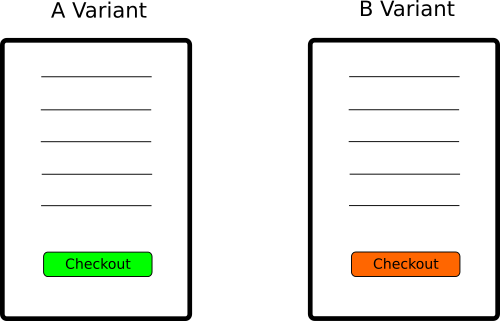
一周后我们收集到如下数据：

	转化	总计
变量A	100	10000
变量B	120	10000

如果这个时候你就认为变量B的表现优于A，那么你正在使用一个非常幼稚的方法。由于实验的内在随机性，实验结果可能每周都会发生变化。简单的说，你可能完全错了。一个更全面的方法是根据我们测量所获得数据估计变量B的可能性比变量A更好，同时统计是这项工作中最好的工具。

统计建模

统计学家喜欢用猜测瓶子中球的数量来举例，我们的问题可以用从两个不同的瓶子中提取球来模拟。每个瓶子都有一定比例的红球和绿球。红球表示付款成功，绿球表示未付款离开。

在属于变量B的瓶子中的红球的比例比属于变量A的瓶子的红球比例更大吗？通过从瓶子中进行可放回的抽样来估计红球的比例。我们从每个瓶子中抽取一定数量的球并计算比例。每次抽取一个球后都在将球放回瓶后再进行第二次抽取，以保持瓶中球的比例不发生变化。

                                                   --变量A

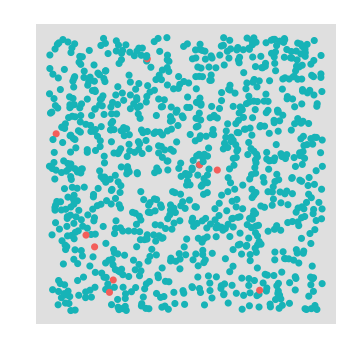
                                                   --变量B

现在好消息是二项分布能够准确的模拟这种实验。它能告诉在独立的yes/no实验中每次提取n中的预期成功数，并且生成一个成功数的概率P。

换句话说，每次从瓶子中取n个球，红球代表yes，绿球代表no。二项分布计算从n个球中拿个k个红球的概率。如下所示：

(a) $Pr(X = k) = \frac{n!}{k!(n-k)!} p^k (1-p)^{n-k}$

利用R中的dbinm()来验证。假设一个瓶子中红球的概率是30%，提取100个球其中有10个红球的概率是多少？ $Pr(X = 10)$ 如下：

dbinom(10, 100, 0.3)

1.17041796785404e-06

结果非常小。好吧，瓶子中其实定义了更大比例的红球，我只是不走运的抽到比已定比例少的红球。现在我们画出红球数从0到100的概率值变化：

x = 1:100

y = dbinom(x, 100, 0.3)

options(repr.plot.width=7, repr.plot.height=3)

qplot(x, y, xlab=”Number of successes”, ylab=”Probability”) + xlim(0, 60)

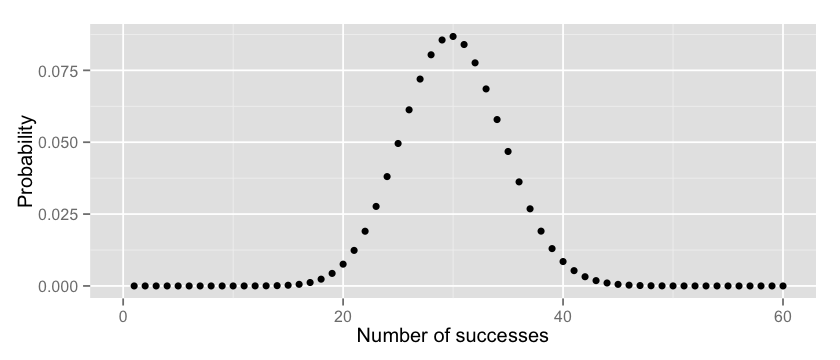
有道理的，不是吗？较大概率获取准确成功数在30左右，就是假设里我们瓶子中红球的比例。

幼稚实验方法的评估

让我们回到开头的那张数据表（包含转换和总计的那张表）。

其中一个评估B是否比A好的方法是画期望分布。假设A是服从p=0.01的二项分布(在10000次尝试中我们有100次转换)，B是服从p=0.012的二项分布(在10000次尝试中我们有120次转换)。下面是代码：

x_a = 1:10000

y_a = dbinom(x_a, 10000, 0.01)

x_b = 1:10000

y_b = dbinom(x_b, 10000, 0.012)

data = data.frame(x_a=x_a, y_a=y_a, x_b=x_b, y_b=y_b)

options(repr.plot.width=7, repr.plot.height=3)

cols = c(“A”=”green”,”B”=”orange”)

ggplot(data = data)+ labs(x=”Number of successes”, y=”Probability”) + xlim(0, 200) + geom_point(aes(x=x_a, y=y_a, colour=”A”)) + geom_point(aes(x=x_b, y=y_b, colour=”B”)) + scale_colour_manual(name=”Variants”, values=cols)

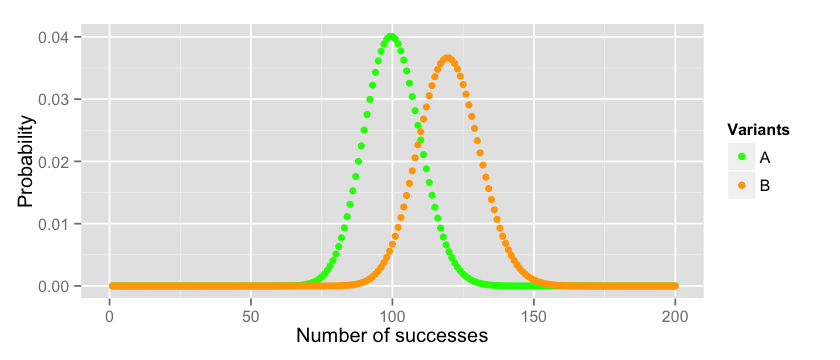
所以如果两个分布的真实成功概率分别是 $p_a = 0.01$ 和 $p_b = 0.012$ ，那么我们可以说B的表现比A好。如果我们重复实验A几次(总计10000)，我们获得的值大部分在70和129之间。同理，B获取的值大部分在87到152之间。你能画图验证这些边界或是根据拇指定律计算边界。

n=10000; p=0.01; q=1-p; mean=100

paste(mean - 3 * sqrt(npq), “,” ,mean + 3 * sqrt(npq)) n=10000; p=0.012; q=1-p; mean=120

paste(mean - 3 * sqrt(npq), “,”, mean + 3 * sqrt(npq))

但是等一下我们怎么知道 $p_a = 0.01$ 和 $p_b = 0.012$ 是真实的呢？最后我们只做了一次提取(只做了一次实验)。如果这些数字是错的，我们的分布将发生变化，前面所做的分析也将存在缺陷。我们能做的更好吗？

更严格的实验评估

应用中心极限定理估计变量的均值。中心极限定理的简单定义：独立随机变量的和趋向于正态分布。

我们想估计变量成功比例均值的分布。假设你运行A/B测试N=100次，每次收集总数n=10000个样例，你会得到变量A如下的成功比例：

$p_a^1, p_a^2 ... p_a^N$

根据中心极限定理得到比例均值的分布和其中的参数。

$\sigma_p = \frac{\sigma}{sqrt(n)} * \frac{N-n}{N-1} \approx \sqrt{\frac{p * (1-p)}{n}}$

其中 $\sigma = \sqrt{p * (1-p)}$ 是正态分布的标准差。

回到我们的问题， $p_a$ 和 $p_b$ 的真实值是什么？我们真的不知道，但他们的分布如下：

x_a = seq(from=0.005, to=0.02, by=0.00001)

y_a = dnorm(x_a, mean = 0.01, sd = sqrt((0.01 * 0.99)/10000)) x_b = seq(from=0.005, to=0.02, by=0.00001)

y_b = dnorm(x_b, mean = 0.012, sd = sqrt((0.012 * 0.988)/10000)) data = data.frame(x_a=x_a, y_a=y_a, x_b=x_b, y_b=y_b)

options(repr.plot.width=7, repr.plot.height=3)

cols = c(“A”=”green”,”B”=”orange”)

ggplot(data = data)+ labs(x=”Proportions value”, y=”Probability Density Function”) + geom_point(aes(x=x_a, y=y_a, colour=”A”)) + geom_point(aes(x=x_b, y=y_b, colour=”B”)) + scale_colour_manual(name=”Variants”, values=cols)

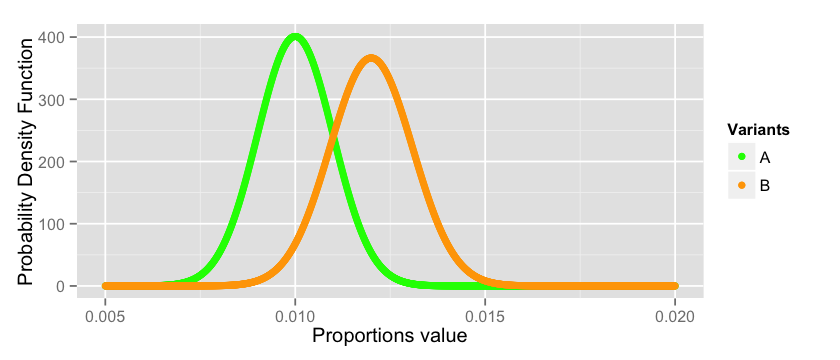
正如您所看到的，我们正在处理一件有风险的工作。有很大几率 $p_a$ 和 $p_b$ 的真实均值的估计值是错误的，因为他们能是分布中的任何值。其中的某个值会认为 $p_a$ 的表现比 $p_b$ 好，与我们上面所得结论相违背。这里没有很好的方法解决这个问题，因为这是概率世界的内在本质问题。但是我们可以尽最大的努力去度量这个风险并得到一个合理的结论。

定量评价

在前面的部分，我们看到变量B很可能比变量A表现的好，但是我们如何度量这句表述？在这个问题中有不同的方法，但这些方法都用到统计假设。

这里省略了一段假设概率的发展史，我想没人去看这些paper的吧！–=

在这个框架中，我们规定一个零假设，并且通过观测数量来尝试拒绝它。在我们的例子中假设真实的转换概率是 $p_a$ ，而 $p_b$ 是随机出现的结果。换句话说我们假设真实世界的用户表现和变量A一样，我们想知道在这个假设下变量B表现(转换数)的概率。

所以，如果二项式的成功概率是 $p_a = 0.01$ ，转换数大于等于120的概率是多少？我们只需要将所有可能出现事件的概率相加：

当计算这个值时你可以使用模式(a)中的概率密度函数或用R：

binom.test(120, 10000, p = 0.01, alternative = “greater”)

下面是结果：

data: 120 and 10000

number of successes = 120, number of trials = 10000, p-value = 0.0276

alternative hypothesis: true probability of success is greater than 0.01

95 percent confidence interval:

0.01026523 1.00000000

sample estimates:probability of success :0.012

在R函数中设置alternative = “greater”来计算转换数大于120的几率。但是我们还有其他的方法来解决这个问题。P值可以准确的表示能够获得大于120个成功数的概率。例如 $P(X_a >= 120)$ .下图在变量A的分布中将p值表示的部分标记出来了。

x_a = 1:10000

y_a = dbinom(x_a, 10000, 0.01) data = data.frame(x_a=x_a, area=append(rep(0, 119), seq(from=120, to=10000, by=1)), y_a=y_a) options(repr.plot.width=7, repr.plot.height=3)

ggplot(data = data)+ labs(x=”Number of successes”, y=”Probability”) + xlim(50, 150) + geom_point(aes(x=x_a, y=y_a)) + geom_area(aes(x=area, y=y_a), colour=”green”, fill=”green”)

Type I 和 Type II 错误

Type I 和 Type II 错误和机器学习中的False positive 和 False negative定义相似。

Type I是当零假设是正确时拒绝零假设的概率。在我们的例子中这种情况发生在当实际A/B测试无效但我们却得到A/B测试有效的结论。

Type II是当零假设是错误时接受零假设的概率。在我们的例子中这种情况发生在当实际A/B测试有效时但我们却得到A/B测试无效的结论。

在上面例子中binom.test函数返回的P值就是用来度量Type I错误发生的概率。为了去度量Type II错误，我们需要知道我们愿意以多大的概率 $pvalue = \alpha$ 来拒绝零假设。这里通常都设置 $\alpha = 0.05$ .

当 $\alpha = 0.05$ 时我们拒绝零假设的最小转换数是多少？如下所示：

$P(X <= x_{\alpha}) = 1 - \alpha$

利用R可以简单计算：

alpha = 0.05

qbinom(1 - alpha, 10000, 0.01)

117

现在我们知道从117+1个转换数开始来拒绝零假设。

为了计算Type II错误我们需要假设零假设是错误的，并且度量当转换数是117或更少时我们犯错的可能性。

$P(X_b <= 117) = P(X_b = 0) + P(X_b = 1) ... + P(X_b = 117)$

如下：

pbinom(117, 10000, 0.012)

0.414733285324603

这里的意思是约有40%的几率当我们得到实验无效的结论时真实情况却是有效的。

这似乎过于严厉了。我们能做什么？获取更多的数据是最先要尝试的方法。如果我们获取20000的数据并进行相同的计算，Type II错误会大大降低。

qbinom(0.95, 20000, 0.01) :critical value at which we reject the null-hypothesis

223

pbinom(223, 20000, 0.012) :type II error

0.141565461885161

这里的意思是有14%的几率当我们得到实验无效的结论时真实情况却是有效的。我们甚至能看不同数据下的Type II 错误的变化情况，如下所示：

v = c(); n = 1000:50000

for(i in n) {

critical = qbinom(0.95, i, 0.01)

t2_error = pbinom(critical, i, 0.012)

v = append(v, t2_error)} options(repr.plot.width=7, repr.plot.height=3)

qplot(n, v, xlab=”P(type II error)”, ylab=”Observations”)

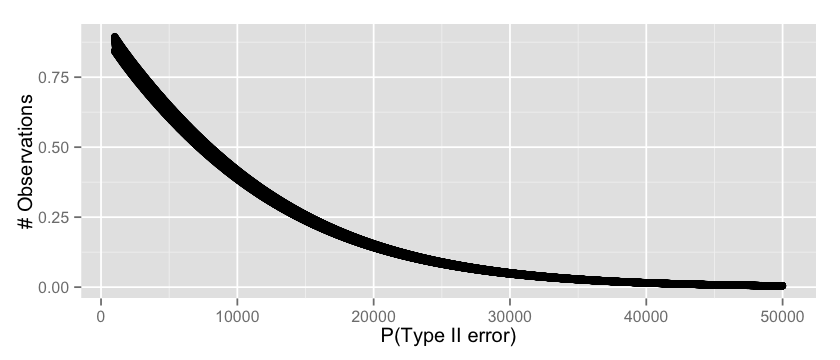
这似乎是一个合理的结果，从30000开始我们能万无一失的假设我们的概率，即Type II错误将很低。

上面提到的分析中，它的基础假设是有缺陷的。当估计Type I错误时我们假设 $p_b$ 是0.012而当估计Type II错误时我们假设 $p_a$ 是0.01。我们从极限定理可知这是不准确的，因为这些值分布在某个区域内。所以让我看看如果我们从分布中去几个点会发生什么事情。例如1%，25%，50%，75%，99%，并检查我们的假设检查错误发生了什么。

对于Type II错误，我首先收集 $p_a$ 的所以可能值：

mean = 0.01

sigma = sqrt((mean * 0.99)/10000)

p_a_values = c(

qnorm(0.01, mean = mean, sd = sigma),

qnorm(0.25, mean = mean, sd = sigma),

qnorm(0.50, mean = mean, sd = sigma),

qnorm(0.75, mean = mean, sd = sigma),

qnorm(0.99, mean = mean, sd = sigma))

p_a_values

然后我准确的估计错误：

parametric Type II

count = 50000; start = 1000

data = data.frame(x= numeric(0), error= numeric(0), parametric_mean = character(0))

p_a_values = factor(p_a_values) for(p_a in p_a_values) {

n = start:(start+count)

x = rep(0, count); error = rep(0, count); parametric_mean = rep(‘0’, count);

for(i in n) {

p_a_numeric = as.numeric(as.character(p_a))

critical = qbinom(0.95, i, p_a_numeric)

t2_error = pbinom(critical, i, 0.012)

index = i - start + 1

x[index] = i

error[index] = t2_error

parametric_mean[index] = p_a}

data = rbind(data, data.frame(x = x, error = error, parametric_mean=parametric_mean))} options(repr.plot.width=7, repr.plot.height=3)

ggplot(data=data, aes(x=x, y=error, color=parametric_mean, group=parametric_mean)) + geom_line()

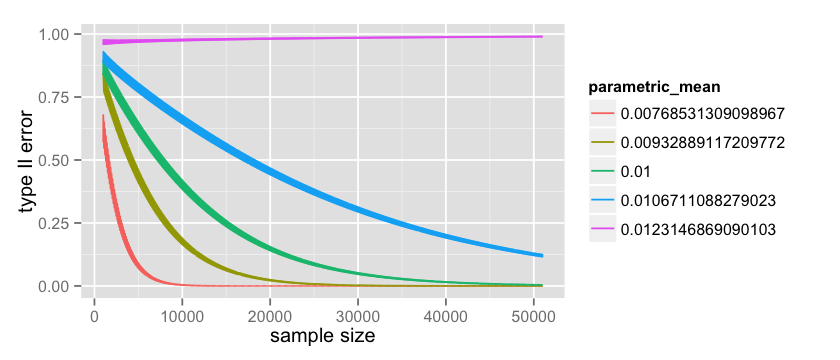
这里的绿线和上面所画的线是相同。观测 $p_a=0.0123$ 的那条线是相当有意思的。这是一个更坏的情况，因为我们取了一个比 $p_b=0.012$ 大的值，因为这个我们的Type II错误随着观测数实际是增加的。但是值得一提的是这个值是不可能的，因为数据收集的越多 $p_a$ 值的不确定性越小。你能看到图中的线是很厚的，这是因为离散检验具有相当大的波动性。

同理我们可以将它应用到Type I错误。前面我们看到可以用 binom.test()函数计算，但是我们也可以手工计算，如下(当 $p_a=0.01$ ， $Pb=0.012$ ):

pbinom(119, 10000, 0.01, lower.tail=FALSE)

从119开始我们接受零假设。代码如下：

parametric Type I

count = 50000

start = 1000

data = data.frame(x= numeric(0), error= numeric(0), parametric_mean = character(0))

p_b_values = factor(p_b_values)

for(p_b in p_b_values) {

n = start:(start+count)

x = rep(0, count); error = rep(0, count); parametric_mean = rep(‘0’, count);

for(i in n) {

p_b_numeric = as.numeric(as.character(p_b))

expected_b = i * p_b_numeric

t1_error = pbinom(expected_b - 1, i, 0.01, lower.tail=FALSE)

index = i - start + 1

x[index] = i

error[index] = t1_error

parametric_mean[index] = p_b }

data = rbind(data, data.frame(x = x, error = error, parametric_mean=parametric_mean))}

options(repr.plot.width=7, repr.plot.height=3)

ggplot(data=data, aes(x=x, y=error, color=parametric_mean, group=parametric_mean)) + geom_line()

就像Type II错误，我们注意到当 $Pb=0.009$ 时，随着数据的增长，Type I错误变大。但是这个值是不可能出现的。

这里有个有意思的事情是两类错误以不同的速率下降。整体来看，根据这个设计，我们更多的坚持认为按钮颜色的改变无影响。当现实上按钮颜色无影响时，大部分次数的测试会显示按钮无影响。当现实上按钮颜色有影响时，测试有很大的风险会说两者无区别(Type II错误下降很慢)。

估计样本容量

为了确保实验结果具有统计显著性，我们如何估计实验的运行时间呢？你只需要从不同的角度来使用同样的工具就能解决这个问题。

首先你需要根据当前的转换基线做一个转换估计值。如果你使用google analysis你可以简单的获取绿色按钮的转换率。

第二，你需要对效应值做一个猜测。在我们的例子中选择效应值为20%。关于效应值的解释可以看这两,篇

第三，你需要确定你愿意在Type I错误上冒多大的风险，即选择 $\alpha$ 值。

最后，你需要确定你愿意在Type II错误上冒多大的风险，即当橙色按钮有效时你愿意以多大的概率去说这个橙色按钮无效。这相当于当橙色按钮实际有效时，你有多大的权利去断定橙色按钮是有效的。

下面是计算效应值的步骤：

首先，我看一下统计：

$\delta = |p_a - p_b|$

然后我们用如下的公式计算样本大小n：

(1) $P(reject H0 / H0 is true)=\alpha$

(2) $P(reject H0 / H0 is false) = power = 41 - \beta$

现在你必须有一些业务上的直觉。 $\delta$ 最小值会是多少？你可以想象最小效应值是(1)和(2)的函数。(1)中的最小值是：

$z_{1-\alpha} * \sqrt{\frac{p_a * (1-p_a)}{N}}$

(2)的最小值是：

$z_{1-\beta} * \sqrt{\frac{p_b * (1-p_b)}{N}}$

当 $power = 1 - \beta$ ，我们可以得到：

$\delta_{min} = z_{1-\alpha} * \sqrt{\frac{p_a * (1-p_a)}{N}} +z_{1-\beta} * \sqrt{\frac{p_b * (1-p_b)}{N}}$

可以得到N为：

$N = (\frac{ z_{1-\alpha} * \sqrt{p_a * (1-p_a)} + z_{1-\beta} * \sqrt{p_b * (1-p_b)}}{\delta_{min}})^2$

所以使用上面的方法：(i)绿色按钮的基准转换率是1%；(ii)效应值为20%，那么橙色按钮的转换率为1.2%；(iii)接受Type I错误的概率为5%(iv)设置power为80%。转换为R语言为：

p_a = 0.01

p_b = 0.012

alpha = 0.05

beta = 0.2

delta = abs(p_a - p_b)

t_alpha = qnorm(1 - alpha)

t_beta = qnorm(1 - beta)

sd1 = sqrt(p_a * (1-p_a))

sd2 = sqrt(p_b * (1-p_b))

n = ((t_alpha * sd1 + t_beta * sd2) / abs(p_a - p_b))^2

这看起来似乎与我们先前的模拟一样。但另一方面比用注明的A/B测试工具测量的值低30%。作者不清楚原因。

A/B测试详解

介绍

统计建模

幼稚实验方法的评估

更严格的实验评估

定量评价

Type I 和 Type II 错误

估计样本容量

FEATURED TAGS