本人能力有限，翻译只是为了更好的理解，如有错误欢迎指正。

本文翻译自《7 Important Model Evaluation Error Metrics Everyone should know》

七个重要的模型误差度量

你的目的不仅仅是构建一个预测模型，而是创建和选择一个对样本以外的数据同样具有高度精度的模型。因此在用模型计算预测值之前，去检测模型准确度是非常重要的一个步骤。

目录：

1. 混淆矩阵（Confusion Matrix）
2. 增益和提升图（Gain and Lift Chart）
3. K-S图（Kolmogorov Smirnov Chart）
4. AUC – ROC
5. 基尼系数（Gini Coefficient）
6. Concordant – Discordant Ratio
7. 均方根误差（Root Mean Squared Error）
8. 交叉验证（Cross Validation (Not a metric though!)）

提醒：预测模型的类型

回归模型（输出是连续的）和分类模型（输出是标称数据[离散数据]或二分数据）具有不同的评估度量。

分类问题：

1. 类别输出：SVM和KNN创建一个分类输出。例如，在二分类问题中，输出可能是0或是1。但是，现在有一些算法可以将类别输出转换为概率。然而这些算法在统计学界不太被认同。
2. 概率输出：逻辑回归、随机森林、梯度提升（Gradient-Boosting）、Adaboost是概率输出的。转换概率输出到类别输出只是创建一个阈值概率的问题。

在回归问题中，输出总是连续的不需要再进一步处理。

1. 混淆矩阵（Confusion Matrix）

混淆矩阵是一个N X N的矩阵，N是预测类别的数目。如下表所示：

Model&Target	Positive	Negative
Positive	True Positives(TP)	False Positives(FP)
Negative	False Negatives(FN)	True Negatives(TN)
tota;	Positive Sample(P)	Negative Sample(N)

• Accuracy = (TP+TN)/(P+N) ：预测正确的数目占总数的比值
• Positive Predictive Value = Precision = TP/(TP+FP)：模型预测Positive中正确占比
• Negative Predictive Value = TN/(TN+FN)：模型预测Negative中正确占比
• True Positive Rate = Recall = Sensitivity = TP/P：在实际Positive例子中模型预测正确占比
• True Negative Rate = Specificity = TN/N ：在实际Negative例子中模型预测正确占比

这里用R中ROCR例子做代码示例：

数据展示，其中prediction是预测值，labels为真实值。

library(ROCR)
data(ROCR.simple)
data <- as.data.frame(ROCR.simple)

创建一个prediction对象,并画出Accuracy、Positive Predictive Value、Negative Predictive Value、Sensitivity、Specificity。

pred <- prediction(ROCR.simple$predictions,ROCR.simple$labels)
par(mfrow = c(2, 3), pty='m')
Accuracy <- performance(pred, 'acc')
plot(Accuracy)
Ppv <- performance(pred, 'ppv')
plot(Ppv)
Npv <- performance(pred, 'npv')
plot(Npv)
Tpr <- performance(pred, 'tpr')
plot(Tpr)
Tnr <- performance(pred, 'tnr')
plot(Tnr)

从以上各图可以看到随着cutoff(门槛值)变化，各指标也发生变化。通常情况下我们只考虑其中的一个指标，例如药物实验中，可能更多的关注Specificity。在一个预测用户流失的模型中，可能更多的关注sensitivity。

或是使用caret包中的confusionMatrix函数计算混淆矩阵

library(caret)
#设置positve为1
confusionMatrix(cft, positive = "1")
#confusionMatrix(pred.class, ROCR.simple$labels, positive = "1")

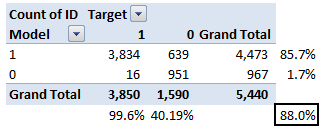上面是原文的例子，准确度为88%。从上表可以看出，阳性(positive)预测值很高，阴性(negative)预测值却很低。同样灵敏度(Sensitivity)很高，特异性(Specificity)却比较低。这主要是由于我们所选的门槛值造成的。如果我们增大门槛值，两对值差距会变大。

2. 增益和提升图（Gain and Lift charts）

lift计算公式为 Positive Predictive Value和(True Predictive Positives+False Predictive Negatives)/all observations的比值，这个指标衡量的是应用模型后比不使用模型的效果有多大提升。当不使用模型时我们需要从所有样本估计正例的比例，当使用模型后我们只需要从预测的正例估计正例的比例，样本 范围缩小了。

gain计算公式为True Positive Rate。

增益和提升图主要是检查概率的排序。下面是建立增益和提升图的步骤：

1. 计算每个观察值的概率
2. 降序排列这些概率
3. 构建十分位数分析，即将观测值以每10%的数目分一组（十分位数非必须，一般多用于信用评分模型的建立）。
4. 计算每个分组内的反应率和累积反应率（Good (Responders) ,Bad (Non-responders) and total）

例如你在进行某项用户召回活动的策划，在以往的活动中用户成功召回的的概率为10%，然后你根据以往活动的用户数据建立模型(也可以简单的根据关键指标排序：例如交易金额或活跃度)，并按照上面步骤计算。那么如果你选出前30%的用户发现成功召回用户占比30%， 则对这30%的用户群体，模型的提升度为30%/10%=3倍，也就是运用模型挑选的用户召回成功率高三倍。

应用上篇混淆矩阵中的prediction(ROCR包)对象创建lift图：

lift <- performance(pred, measure="lift", x.measure="rpp")
plot(lift, main = "Lift Chart")

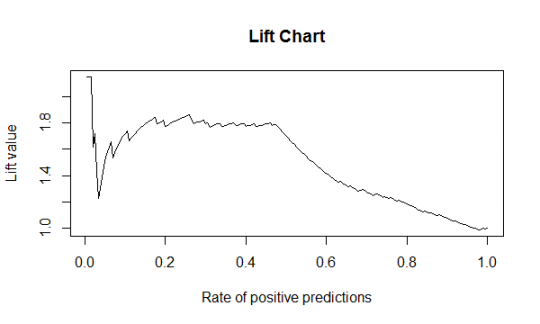如图所示当Positive Predictive Value比例越小，lift提升度越高。也就是门槛值设计越高(将更少的预测Positive归于实际Positive)，这一小部门 预测Positive准度度越高(和实际Positive特征最接近)。最后一般选择从右向左上升期中最陡峭的点。

gain <- performance(pred, "tpr", "rpp")
plot(gain, main = "Gain Chart")

如图所示当Positive Predictive Value比例越大，gain越高。最后一般选择从左向右上升期中最陡峭的点。

原文中的表如下，可以据此画出提升图：

这是一个非常有用的表。累积增益图是 Cumulative %Right 和 Cummulative %Population之间的图。图如下所示：

这个图告诉你，你的模型是如何将反应人群和非反应人群区分的。例如，第一个十分位数有整体的10%，有14%的反应人数。这意味着我们在第一个十分位数有140%的提升。

我们在第一个十分位数所能达到的最大提升是什么？从上面的第一张表，我们知道总共的反应人数为3850.第一个十分位数包含543个观测值。因此，在第一个十分位数的最大提升为543/3850~14.1%。因此，我们非常接近完善这个模型。

现在让我们画提升曲线。提升曲线是上表中total lift和各%population间的关系曲线图。注意对一个随机模型，这里总保持100%的平稳。下面是这个例子的图：

你也可以画出decile wise lift with decile number ：

这个图告诉我们什么？它告诉我们直到第七个分位数模型表现的很好。每个十分位数将向无反应者偏斜。任何模型 lift @ decile在100%上（最小到第三十分位数，最大到第七十分位数）是一个好的模型，否则你可能要考虑先进行抽样。

增益提升图被广泛用在有针对性活动的问题上。它告诉我们在哪个部分我们可以为某个具体的活动定位客户。同样，它告诉你在新的目标基准上你的期望回应是多少？

3. K-S图

K-S图衡量分类模型的表现。更准确的说，K-S是the positive and negative分布之间分离程度的衡量。如果K-S 是100，那么 按分数将整体分成两组，一组包含全部的positive，一组包含全部的negative。 另一方面，如果模型不能区分the positive and negative，那么就像模型从总体中随机选择例子，则K-S会是0。在大多数分类模型中，K-S会落在0到100之间。K-S值越高，模型的分离程度越好。

原文中例子如下表：

我们也可以画%Cumulative Good and Bad看最大的分离。下面是一个简单图：

上面这些度量主要用于分类问题，下面让我们学习新的重要的度量。

4. ROC曲线下面积

这是另一个在工业界流行使用的度量。使用ROC最大的优点是在反应者的比例里是独立变化的，即样本中positive比例的变化不会引起ROC曲线的变化，不同的样本可能具有不同的比例AUC-ROC是在实际数据分析中最常用的的模型误差度量指标，因为在实际的数据集中类的数目往往是不相等的，通常偏差很大，即是不平衡数据集，而且测试数据集中不同类的。分布也会发生变化，应用ROC曲线可以忽略这种变化对模型评估的影响，即ROC曲线不随类别样本分布的变化而变化。 下面的部分会让你清楚这句表述。

让我们先理解什么是ROC曲线，如果我们看下面的混淆矩阵，我们观察一个概率模型，为每个度量获取不同的值。

因此，对于每个灵敏度sensitivity，我们获得一个不同的specificity。下面是两个不同的曲线：

这个ROC曲线是灵敏度sensitivity和（1- specificity）画成的。(1-specificity)是false positive rate and ，sensitivity是True Positive rate。下面是ROC图：

让我们设置门槛值为0.5，下面是混淆矩阵：

正如你所看到的，在这个门槛值下灵敏度是99.6%，(1- specificity)是60%。这个坐标点在我们的ROC曲线上。把这个曲线变成到一个单一的数字，我们定义在ROC曲线下的面积，称为AUC。

注意整体的面积是1。因此AUC是曲线面积和整体面积的比。这个例子的AUC是96.4%。下面是一些经验法则：

• .90-1=excellent(A)
• .80-.90=good(B)
• .70-.80=fair(C)
• .60-.70=poor(D)
• .50-.60=fail(F)

在当前模型下，我们处在excellent。但这可能只是过度拟合。因此在这个例子中使用交叉集做验证是非常重要的。

需要记住的要点：

1. 作为类别输出的模型，在ROC图上将会只有一个单点，因为以类别为输出的模型不会有门槛值区分类别。
2. 判断两个不能互相比较的模型需要采用一个单一的指标而不是多个指标。一个参数是（0.2,0.8）的模型和参数是（0.8,0.2）的模型可能是来自同一个模型，因此这些指标不能被直接比较。
3. 在概率模型下，我们能获取到一个单一的指标（AUC-ROC）。但是我们仍然需要看整体的曲线来获得最终的决定， 因为这里也可能在某些区域某个模型表现的更好，在其他区域另一个模型表现的更好。

使用ROC而不使用提升曲线的原因:

lift 依赖于total response rate of the population，因此如果total response rate of the population改变，同样的模型将会得到不同的提升表。ROC曲线依赖于sensitivity和specificity，这两个变化是同步的，因此不会影响ROC曲线的变化。

这里用R中ROCR中的例子演示，画出sensitivity和specificity随不同门槛值相互变化的曲线图，并据此做出ROC曲线，计算出AUC值。

tpr <- performance(pred, 'tpr')
plot(tpr, ylab='', main='Sensitivity/Specificity')
tnr_x <- performance(pred, 'tnr')@x.values
tnr_y <- performance(pred, 'tnr')@y.values
lines(tnr_x[[1]], tnr_y[[1]])

roc <- performance(pred, measure="tpr", x.measure="fpr")
plot(roc, main = "ROC Chart")
lines(seq(0,1,0.2),seq(0,1,0.2))

auc <- performance(pred, "auc", fpr.stop=1)@y.values
auc

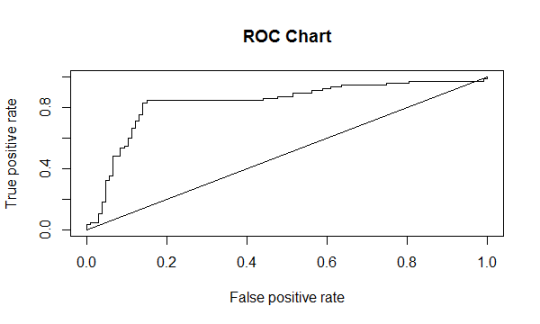从上图中可以看到每一个True Positive Rate，对应一个True Negative Rate(即false positive rate)，两者在不同门槛值下的值组成坐标下(x,y)，并形成ROC曲线图。

5. 基尼系数（Gini Coefficient）

基尼系数有时被用在分类问题。基尼系数可以直接从AUC ROC推得。基尼系数需要AUC值。 Gini = 2*AUC – 1

基尼系数大于60%是一个比较好的模型。在这个例子中基尼系数是92.7%。

6. Concordant–Discordant ratio

这是另一个分类模型中的重要度量。为了去理解这个指标，我们假设有三个学生今年可能通过。下面是我们的预测： A-0.9，B-0.5，C-0.3

如果我们从这些学生中取对，可以得到AB，BC，CA。现在，一年后，A和C通过了，B失败了。现在我们选出一个失败一个成功的对，可以得到AB和BC。这些concordant-pair成功的概率大于失败的概率。而discordant pair是相反的。如果概率相同，我们说它是a tie。让我们看下在我们的例子中： AB-Concordant, BC-Discordant

因此，在这个例子中Concordant是50%，超过60%我们认为是一个好的模型。这个度量一般不会用在决定有多少目标客户。它主要用于评估模型的预测能力。可以用KS、提升图去决定有多少目标客户。

7. 均方根误差（Root Mean Squared Error (RMSE)）

均方根误差是回归模型中最常用的评估指标，它要求模型误差是无偏的，且服从正态分布。以下是这个指标的几个关键点：

1. 均方根误差的平方项能消除偏差间的正负态，也就是说平方使真实值和预测值的偏差完整的保留在这个指标中。
2. 平方根可以使减小这个指标最终值，也就是说让这个指标能展示更多的偏差。
3. 均方根误差避免使用绝对误差项，绝对误差不提倡在数学计算中应用。
4. 样本规模越大，均方根误差越可靠。
5. 均方根误差极易收到异常值的影响，因此如果想利用均方根误差评估模型需要在建模之前处理掉异常值。
6. 和平均绝对误差相比，均方根误差给予误差更高的权重和惩罚。

均方根误差公式为：

N是观察总数。

应用R计算rmse：

predict_value <- rnorm(100)

建立真实值：

actual_value <- rnorm(100)

rmse公式计算：

sqrt( sum( (predict_value - actual_value)^2 , na.rm = TRUE ) / length(actual_value) )

利用rmse函数计算：

rmse(predict_value, actual_value, na.rm = TRUE)

除了这7个指标，还有另一种方法来检查模型的性能。这七种方法是统计学显著的。但是，随着机器学习的到来。我们现在有更稳健的方法来进行模型的选择。它就是交叉验证。虽然交叉验证不是一个真正的评价指标，但它被广泛用来沟通模型的准确性。同时，交叉验证的结果为概括模型的性能提供了一个很好的直观的结果。

8. 交叉验证

交叉验证在任何种类的模型中都是最重要的概念之一。简单的说，就是将训练集再次分成训练集和测试集。

上图展示如何用快速样本验证模型。我们简单的将样本分为两个样本，其中一个建立模型。另一个样本用来快速验证。

上面的方法有消极的一面吗？

训练集减少使这种模型具有高度偏差，并导致模型不会得到最佳估计的系数。所以最好的选择是什么？

如果我们把训练集分成相等的两份，一份用于训练模型，另一份用于验证，然后我们再在另一份训练，一份验证，这种方法被称为2倍交叉验证。

这种方法我们在整体数据上训练模型，但是一次训练一半。

这种方法通过样本选择在一定程度上减少了偏差但却在更少的样本上训练模型。

K折交叉验证

我们从2倍交叉验证扩展到k倍交叉验证。现在，我们可视化k折交叉验证的工作过程。

这是7折交叉验证。

这里是过程：将整体分成7个相等大小的样本。现在我们训练其中的6个，剩下的一个用于验证。然后，我们选择不同的验证集，迭代这个过程7次。在这个过程中，我们在每个样本上训练模型，并在每个样本上做了验证。这是一种在预测中减少选择偏差和方差的方法。一旦我们有了七个模型，我们利用平均误差选择最好的模型。

它是如何发现最好（无过拟合）模型的？

K折交叉验证是广泛被使用来检测模型是否过拟合的。如果性能指标在k次模拟中是相互接近的，指标的均值是最大。

如何在模型中应用k折交叉验证？

原文给出了python代码，这里给出R代码，利用CARET：

library(caret)
data(iris)
TrainData <- iris[,1:4]
TrainClasses <- iris[,5]
fitControl = trainControl(
    method = "repeatedcv",
    number = 2,
    repeats = 2,
    returnResamp = "all")
knnFit1 <- train(TrainData, TrainClasses,
                 method = "knn",
                 preProcess = c("center", "scale"),
                 tuneLength = 10,
                 trControl = fitControl)
summary (knnFit1)

如何选择k？

这是个棘手的部分，我们权衡的选择K。

K如果小了，我们会得到高偏差和低方差。

K如果大了，我们会得到低偏差和高方差。

在大多是时候K选为10.

---

• ← Previous Post
• Next Post →